计算实验金融运用计算机仿真技术来模拟金融市场,通过交易者的微观行为揭示市场的宏观特征,其思想基础和理论方法包括计算实验、复杂性科学、统计物理学、新金融经济学等。计算实验金融学研究是由传统经济学家率先发起的,至少可以追溯到诺贝尔奖得主Stigler在1964年发表的论文[1],并在1990年后分别被金融学家、金融物理学家发扬光大,可谓殊途同归[2]。国外学者对基于经纪人的股市模型研究很多,而国内研究者相对较少。但是,国际上文献报道的研究大多侧重于模型构建和对程式化特征的验证[2],而国内学者对仿真模型在金融工程中的应用研究方面并不落后于国际学界[2][3][4][5],提出了不少原创性的思想,包括股市预测、资产定价、政策建议等方面。天津大学张维教授指出:“虽然目前能够替代CAPM地位的新模型仍未发现,但是计算实验方法开辟了新的途径,为金融学注入了新活力,资产定价的一片崭新天地将出现在我们面前。”在当前的金融经济形势促进下加强对计算实验金融学的研究,或可形成中国学派,领先国际水平。
基于经纪人的微观模型的基本元素是经纪人,市场运行规则既可以是经纪人的局部相互作用,也可以是全局影响因素,或者是二者的耦合[2][6]。几类主要模型包括基本面交易者和噪声交易者博弈模型[7]、逾渗模型[8]、自旋模型[9]、少数者博弈模型[10]等。这几类模型的价格形成由买卖不平衡量决定,因而在一定程度上可以看作是针对报价驱动市场设计的,并且有很大部分模型假设了交易者的某些行为规则(如交易者之间的局部模仿),虽有其合理性,却失之简化,有些甚至没有实证结果支持。
我国股市属于订单驱动市场,采用连续双向拍卖交易机制,因此,从微观上看,上述模型并不适用,应该构建订单驱动模型(或称委托驱动模型或指令驱动模型)。订单驱动模型是一类特殊的基于经纪人的微观模型,可与“沉积-汽化”过程类比[11-13],交易者按照一定的规则下单(沉积)和撤单(汽化),通过自动匹配(汽化)实时更新价格。对订单驱动市场而言,市场机制通过下单和撤单这两个随机过程耦合而成,确定了下单和撤单的规律,即可构建模型模拟股票价格的演化。大部分订单驱动模型仍然采用多种无实证检验的假设,而Mike和Farmer的最新研究[14],则是通过实证研究确定下单和撤单的统计规律,是订单驱动模型建模研究的重要突破。
订单驱动模型是计算实验金融学的一个分支,在金融工程研究中具有很高的潜在应用价值,这方面的研究鲜见有文献报道。通过对订单驱动模型的仿真,可以解决金融工程(包括风险管理和资产定价)中的一些重要问题。
大宗交易的最优下单策略――订单驱动模型可用来研究大宗交易的最优策略问题。王江等人建立的数学模型,假设订单簿的形状具有某种函数形式[15,16],但与实际订单簿形状并不一致[17],因而数学模型给出的最优策略可能并非最优。在建立模拟市场后,我们将可以通过模拟来确定订单簿在大单交易冲击下的恢复行为(resilience behavior),搜索大宗交易的最优下单策略。
期权定价――在传统的资本资产定价理论中,假设收益率的分布是正态的,而实际定价则往往需要通过数值模拟来实现。借助订单驱动模型,对给定股票衍生品的定价将有很大裨益。对于欧式看涨或看跌期权,其价值为
c = max(ST - X, 0)exp[-r(T-t)] (1a)
p = max(X - ST, 0)exp[-r(T-t)] (1b)
我们可以通过模型模拟,生成价格路径,得到标的股票在时刻T时的价格ST,从而得到期权价值的一个估计值。重复多次模拟,得到期权价格的均值即为其期望的估计值。
在险价值(VaR)的估计――在险价值VaR有多种估计方法,如历史模拟法、蒙特卡洛模拟法、方差-异方差法等。通过模型模拟,可以得到统计显著性更高的收益率分布。对这一问题的深入研究,可望开发出精确度更高的VaR估计方法。
股市微观结构理论――通过计算实验研究市场微观结构理论中的一些重要问题,如市场有效性悖论、价格影响函数、收益率幂律尾分布与大波动的成因、部分成交订单和全部成交订单的不同行为、市场的流动性等。
股市泡沫形成机理――在股市中存在大量泡沫,其中很大比例的金融泡沫呈现对数周期性幂律模式,微观模型可能为理解这些特征模式的形成提供线索。
极端股市波动发生时间的预测――收益率时间序列中数值超过某一设定阈值Q的事件被称为极端事件,这些极端事件之间的回复时间τ(return interval)的统计性质对研究股票价格大波动具有重要意义[18]。通过计算回复时间的概率密度PQ(τ),可以得到一个极端事件发生x时间后在Δx内发生另一极端事件的概率WQ(x, Δx) [19]:
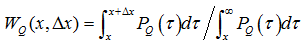 (2)
(2)
进一步地,如果确定了回复时间的条件概率p(τ|τ0),那么,在前一回复时间为τ0且上次极端事件发生x时间的条件下,发生下一极端事件的等待时间为[20]:
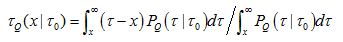 (3)
(3)
这些研究将对金融市场风险管理具有重要价值和指导意义。
参考文献
[1] Stigler G J. J. Business, 1964, 37: 117
[2] 周炜星. 金融物理学导论. 上海: 上海财大出版社, 2007
[3] 刘文财等. 系统工程学报, 2003, 18: 135
[4] Zhang W et al. Int. J. Info. Tech. & Dec. Mak., 2006, 5: 455
[5] 张维等. 管理科学, 2008, 21: 74
[6] Johnson N F, Jefferies P, Hui P M. Financial Market Complexity: What Physics Can Tell Us About Market Behaviour. Oxford: Oxford University Press, 2003
[7] Lux T, Marchesi M. Nature, 1999, 397: 498
[8] Cont R, Bouchaud J P. Macroecon. Dyn., 2000, 4:? 170
[9] Zhou W X, Sornette D. Eur. Phys. J. B, 2007, 55:? 175
[10] Challet D, Marsili M, Zhang Y C. Minority Games: Interacting Agents in Financial Markets. Oxford: Oxford University Press, 2005.
[11] Maslov S. Physica A, 2000, 278: 571
[12] Raberto M. Cincotti S. Physica A, 2005, 355: 34
[13] Farmer J D, Patelli P, Zovko I I. Proc. Natl. Acad. Sci. U.S.A., 2005, 102: 2254
[14] Mike S, Farmer J D. J. Econ. Dyn. Control, 2008, 32: 200
[15] Obizhaeva A, Wang J. J. Fin. Markets, 2009, 16: 1
[16] Alfonsi A et al. Quant. Fin., 2010, 10: 143
[17] Gu G F et al. Physica A, 2008, 387: 5182
[18] Yamasaki K et al. Proc. Natl. Acad. Sci. U.S.A., 2005, 102: 9424
[19] Bogachev M I et al. Phys. Rev. Lett., 2007, 99: 240601
[20] Bunde A et al. Phys. Rev. Lett., 2005, 94: 048701